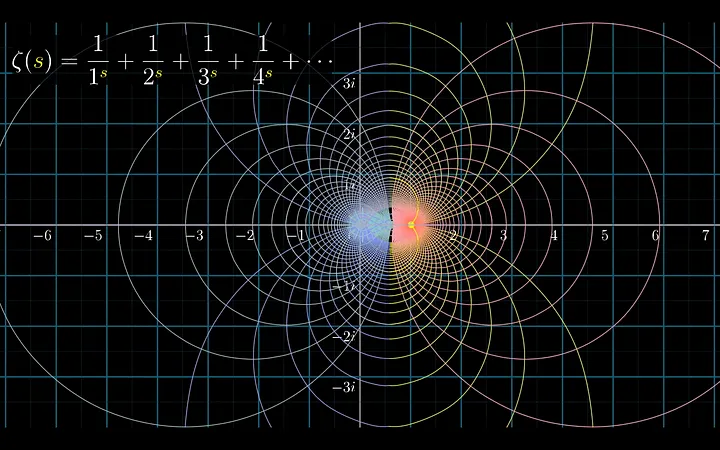
La hipótesis de Riemann
En el año 2000 la fundación Clay de matemáticas fundó los 7 problemas del milenio, los cuales tienen una recompensa de un millón de dólares para la persona que logre resolver un problema, en los que se encuentran: P vs NP, La conjetura de Birch y Swinnerton-Dyer, Yang-Mills y el salto de masa, Las ecuaciones de Navier-Stokes, La conjetura de Hodge, La hipótesis de Riemann y la Conjetura de Poincaré.
En este artículo se profundizará la hipótesis de Riemann formulada por el matemático Bernhard Riemann en el año 1859, describe la cantidad de números primos de un intervalo. Dichos números primos tienen relación con la función zeta de Riemann; la cual tiene dos tipos de ceros, los ceros triviales y los ceros no triviales. Aproximadamente se han calculado diez billones de ceros no triviales y nadie ha podido demostrar que por lo menos un cero esté fuera de la linea de 1/2 o en su defecto nadie ha demostrado que todos los ceros existentes se encuentra en dicha linea.
La hipótesis de Riemann como problema del milenio.
La hipótesis de Riemann, formulada por el matemático Bernhard Riemann en el año de 1859, siendo el ojo de muchos otros matemáticos por su estrecha relación que tiene con la distribución de los números primos con la función zeta de Riemann.
- Ceros triviales. Son los ceros que se obtienen al hacer cero la función seno, los cuales son todos los pares negativos reales, es decir (-2,-4,-6,-8,-10, …). Siendo ζ(2n)=0, donde n no puede ser igual a cero ya que la función zeta no está definida en ese eje.
- Ceros no triviales. Punto del plano complejo cuya parte real se encuentra entre 0<Re<1. Estos ceros se encuentran en el eje de 1/2 también llamada línea critica.
- Banda critica. Rango de la función que se encuentra entre dos puntos que divergen la función zeta, es decir 0<Re<1.
Si la función la consideramos ζ(s)=0, entonces la función diverge.
Si la función la consideramos ζ(s)=1, entonces la función diverge.
“La parte real de todo cero no trivial de la función zeta ζ(s) es ½”
Bernhard Riemann
Definición zeta para valores mayores que 1.
En el plano complejo, la función zeta de Riemann está definida por la siguiente ecuación.
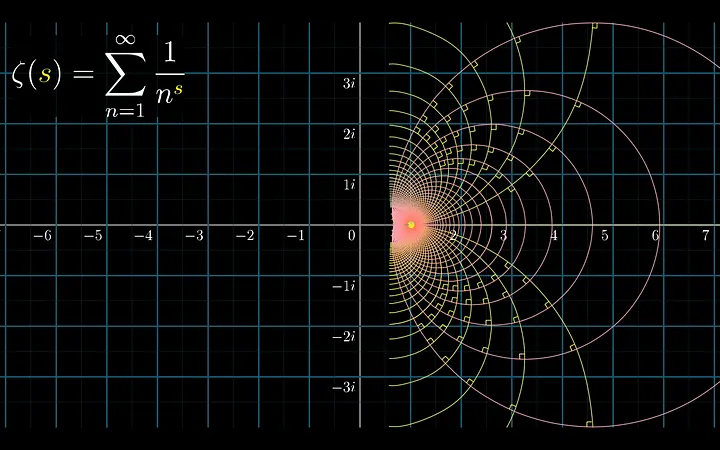
Siendo esta serie estrictamente para valores Re > 1, rango en donde la serie converge en todos los puntos del plano
Demostración.
Como funcionan las potencias complejas
Definamos s=Re y ti, donde Re y t son dos números reales y donde i es la unidad imaginaria
Para s=2
Podemos observar que es el problema de Basilea
Para s=2+i
Definición zeta para valores menores que 0.
La sumatoria solo sirve para valores mayores que 1, más sin embargo se puede expandir el rango de la función usando la extensión analítica de funciones.
La siguiente ecuación nos permite explorar el plano para valores menores de cero, donde necesitamos ∑∞n=1para evaluar ζ(1-s).
Ceros triviales
En la ecuación se encuentra la función “sin(πs/2)” con rango {Re(s)< 0}, entonces se deduce que todos los pares negativos hacen cero la función zeta de Riemann (-2,-4,-6,-8,-10, …). Siendo ζ(2n)=0, donde n no puede ser igual a cero ya que la función zeta no está definida en ese eje.
Definición zeta para valores entre la banda critica.
En la banda critica no existe una ecuación que nos ayude a visualizar la función, ni siquiera usando la extensión analítica.
Supongamos s=1/2
Llegamos a la contradicción que para evaluar ζ(s)=1/2, necesitamos la función evaluada en sí misma, donde tampoco se puede usar ∑∞n=1 (1/ns), ya que Re(s) > 1
Ceros no triviales
No existe una ecuación directa que nos ayude encontrar dichos ceros, pero podemos aproximarnos mediante métodos numéricos y para demostrar que sea verdad podemos usar las ecuaciones de “Euler-Maclaurin” y “Riemann-Siegel”, con las que nos demuestran su validez del punto.
“La parte real de todo cero no trivial de la función zeta ζ(s) es ½”
Bernhard Riemann
Euler-Maclaurin
Riemann-Siegel
Demostración para el primer rho
El primer cero no trivial, también llamado primer rho, tiene un valor de ζ(1/2+14.134725141734694…i)
Para θ(t)
Para P y N
Donde N=1 y R=0.4998704529233008
Para C0, C1 ,C2 ,C3
Para R
Evaluado en ζ(1/2+it)
Aplicaciones de la función zeta de Riemann.
Sabiendo que la función zeta de Riemann tiene una pequeña correlación con los números primos, siendo de mayor importancia para la teoría de números, donde podemos determinar el número de primos por debajo de un intervalo.
donde π(x) es una función para calcular los números primos
Para R
donde p son los ceros no triviales.
| x | π(x) | π(x)-x/ln(x) | li(x) – π(x) |
| 10 | 4 | -0.3 | 2.2 |
| 102 | 25 | 3.3 | 5.1 |
| 103 | 168 | 23 | 10 |
| 104 | 1,229 | 143 | 17 |
| 105 | 9,592 | 906 | 38 |
| 106 | 78,498 | 6,116 | 130 |
| 107 | 664,579 | 44,158 | 339 |
| 108 | 5,761,455 | 332,774 | 754 |
| 109 | 50,847,534 | 2,592,592 | 1,701 |
| 1010 | 455,052,511 | 20,758,029 | 3,104 |
si la hipótesis de Riemann fuera cierta, tendríamos la mayor aproximación de números primos por debajo de un intervalo x
Referencias
Rodríguez, D. (2018, 28 marzo). Visualización de la función ZETa de Riemann y su extensión analítica. Medium. https://medium.com/sadasant/visualizaci%C3%B3n-de-la-funci%C3%B3n-zeta-de-riemann-y-su-extensi%C3%B3n-anal%C3%ADtica-1de6cb9df327.
Invitado, C. (2014, 26 mayo). El problema cuya solución quizás la conozcan en el cielo – Naukas. Naukas. https://naukas.com/2014/05/26/el-problema-cuya-solucion-quizas-la-conozcan-en-el-cielo/#:~:text=Los%20ceros%20no%20triviales%20son,%CE%B6(z)%20es%20cero.
Rodríguez, H. (2022b, septiembre 16). Los 7 problemas matemáticos del millón de dólares. www.nationalgeographic.com.es. https://www.nationalgeographic.com.es/ciencia/7-problemas-matematicos-millon-dolares_18751.
Jean-Marie De Koninck and Florian Luca. Analytic number theory: Exploring the anatomy of integers, volume 134. American Mathematical Soc., 2012.
Bernhard Riemann. Ueber die anzahl der primzahlen unter einer gegebenen grosse. Ges. Math. Werke und Wissenschaftlicher Nachlaß, 2(145-155):2, 1859.