La conjetura de Birch y Swinnerton-Dyer
En el año 2000 la fundación Clay de matemáticas fundó los 7 problemas del milenio, los cuales tienen una recompensa de un millón de dólares para la persona que logre resolver un problema, en los que se encuentran: P vs NP, La conjetura de Birch y Swinnerton-Dyer, Yang-Mills y el salto de masa, Las ecuaciones de Navier-Stokes, La conjetura de Hodge, La hipótesis de Riemann y la Conjetura de Poincaré.
En este artículo se profundizará la Conjetura de Birch y Swinnerton-Dyer. La cual fue planteado en 1965 por los matemáticos británicos Bryan Birch y Peter Swinerton-Dyer. Esta hipótesis aborda el conjunto de soluciones racionales a las ecuaciones que definen una curva elíptica.
Curvas elípticas
Sea k un cuerpo. Una curva algebraica E sobre k es una curva cúbica no-singular f(x, y) = 0 con coeficientes en k, junto con un punto especificado O ”al infinito”.
Siendo su estructura
y2=x3+ax+b, con a y b ∈ k
Imagen 1. Ejemplos de curvas elipticas
Funciones L y su relación con los números primos.
Las funciones L ocupan un lugar central en la teoría de números, desde la demostración del Teorema de los Números Primos en Progresión Aritmética por parte de Dirichlet en 1837, hasta el trascendental artículo de Riemann titulado “Sobre el Número de Primos Menores que una Cantidad Dada” en 1859. Estas funciones reciben su nombre en honor a las series de Dirichlet, de las cuales se originan.
Siendo de la forma:
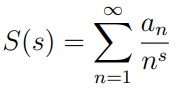
Dicha sucesión nos recuerda a la función seta de Riemann que ya se ha hablado anteriormente https://aeifmx.com/la-hipotesis-de-riemann/
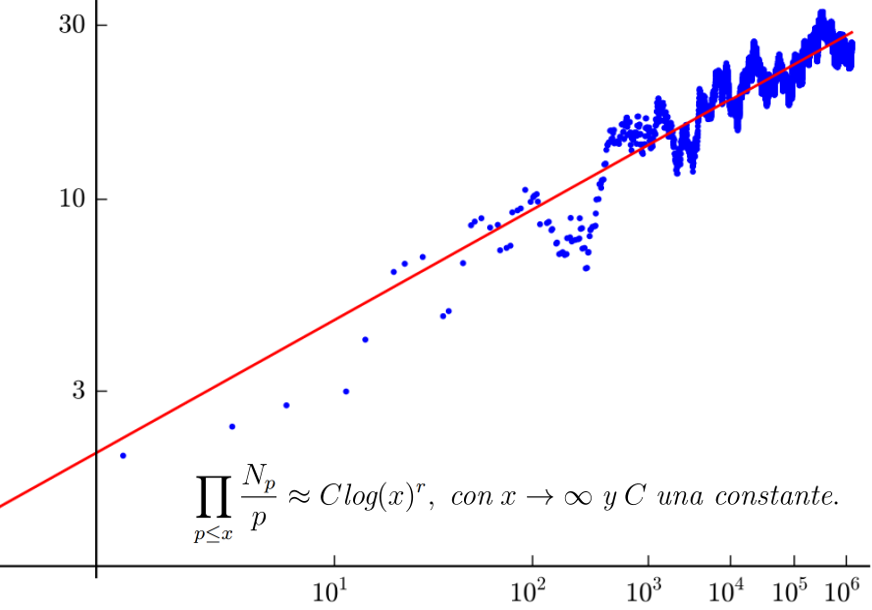
Imagen2. Distribución de primos
Genero de las curvas
- Curvas con infinitos puntos racionales (género 1):
- Si la función L asociada a la curva elíptica tiene un cero de orden par en su punto central crítico, entonces la conjetura predice que la curva tiene infinitos puntos racionales. En este caso, el género de la curva se considera 1.
- Curvas sin puntos racionales (género 0):
- Si la función L no tiene ceros en el punto central crítico, entonces la conjetura sugiere que la curva no tiene puntos racionales. En este caso, el género de la curva se considera 0.
- Curvas con un número finito de puntos racionales (género desconocido):
- Si la función L tiene un cero de orden impar en el punto central crítico, entonces la conjetura es menos específica. No se sabe si la curva tiene un número finito o infinito de puntos racionales. Este caso es más complicado y se considera de género desconocido.
Resolver la hipótesis implicaría encontrar un criterio que permita distinguir entre las diferentes curvas elípticas.
Aplicaciones de la conjetura de Birch y Swinnerton-Dyer
- Teoría de Números y Ecuaciones Diofánticas. La hipótesis está directamente relacionada con las soluciones racionales de ecuaciones diofánticas asociadas a curvas elípticas. Resolver la hipótesis proporcionaría un entendimiento de la distribución de los puntos racionales en tales curvas, lo cual es fundamental en la teoría de números.
- Criptografía. Las curvas elípticas se utilizan en criptografía, y la hipótesis de Birch y Swinerton-Dyer podría tener implicaciones en la seguridad de ciertos sistemas criptográficos basados en estas curvas. Su resolución podría influir en la elección de curvas para aplicaciones criptográficas.
- Geometría Algebraica. La hipótesis está vinculada a la clasificación de curvas elípticas, que son objetos fundamentales en la geometría algebraica. Su resolución podría proporcionar nuevas herramientas y métodos en esta rama de las matemáticas.
- Avances matemáticos. La resolución de la hipótesis abriría el entedimiento de la estructura de las curvas elípticas llevando al desarrollo de nuevas teorías y conceptos matemáticos.
- Influencia en Otras Conjeturas. Su resolución podría tener impacto en otras conjeturas y problemas abiertos en matemáticas, ya que la teoría de números y la geometría algebraica están interconectadas.
- Desarrollo de Algoritmos. La comprensión profunda de las curvas elípticas que provendría de la resolución de la hipótesis podría llevar al desarrollo de algoritmos más eficientes para ciertos problemas matemáticos y computacionales
Referencias
https://www.nationalgeographic.com.es/ciencia/7-problemas-matematicos-millon-dolares_18751
http://www.claymath.org/millennium-problems/birch-and-swinnerton-dyer-conjecture.
Hilbert, David (July 1902). ”Mathematical problems”. Bull. Amer. Math. Soc. 8 (10):
437–479.
An Introduction to the Theory of Elliptic Curves Joseph H. Silverman Brown University
and NTRU Cryptosystems, Inc. Summer School on Computational Number Theory and
Applications to Cryptography University of Wyoming June 19 – July 7, 2006.
Rational points on elliptic curves, Silverman Tate 2015.
An Introduction to the Theory of L-functions J¨orn Steuding (W¨urzburg University). A
course given at Universidad Aut´onoma de Madrid, 2005/06.
Elliptic Curves and the Special Values of L-functions ICTS, 2021 Introduction to Elliptic Curves: Lecture 3 Anupam Saikia Department of Mathematics, Indian Institute of
Technology Guwahati Anupam Saikia IIT Guwahati August 3, 2021.
Los 7 problemas del milenio
https://aeifmx.com/yang-mills-y-el-salto-de-masa-mass-gap/
https://aeifmx.com/la-hipotesis-de-riemann/
https://aeifmx.com/el-problema-de-p-versus-np/

