Yang-Mills y el salto de masa.
En el año 2000 la fundación Clay de matemáticas fundó los 7 problemas del milenio, los cuales tienen una recompensa de un millón de dólares para la persona que logre resolver un problema, en los que se encuentran: P vs NP, La conjetura de Birch y Swinnerton-Dyer, Yang-Mills y el salto de masa <<Mass gap>>, Las ecuaciones de Navier-Stokes, La conjetura de Hodge, La hipótesis de Riemann y la Conjetura de Poincaré.
En este artículo se profundizará el problema de Yang-Mills y el salto de masa. Donde la hipótesis de Yang-Mills estableció los fundamentos de la teoría de las partículas elementales de la materia. En su formulación cuántica, esta teoría describe partículas sin masa, como los gluones. Sin embargo, diversos experimentos han revelado la presencia de lo que los científicos denominan un “salto de masa” o “mass gap”, un fenómeno que aún no se ha observado en la naturaleza pero que está respaldado por la teoría cuántica.
Yang-Mills y el salto de masa como problema del milenio
La aplicación exitosa de esta teoría para explicar las intensas interacciones entre las partículas elementales depende de la existencia de dicho salto de masa. Este fenómeno considera partículas que viajan a la velocidad de la luz, por ende las particulas (gluones) no tienen masa; más sin embargo en la teoría de color cuántica sugiere que para formar estos ligamentos tienen que estar formadas por partículas másicas. La resolución de este enigma implica la búsqueda rigurosa de una formulación cuántica de la teoría de Yang-Mills que pueda dar cuenta de este fenómeno. En otras palabras, se busca determinar si todas las partículas de esta teoría, en particular los gluones, tienen masa o no.
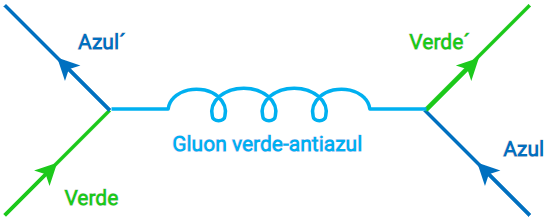
El diagrama anterior describe el comportamiento entre un quark verde y un quark azul, generando así en su interacción el gluón verde-antiazul
Mass gap y la fuerza fuerte.
Para entender el concepto de la fuerza nuclear fuerte, los físicos les gusta compararla con la electromagnética, la cual describe algunos comportamientos similares
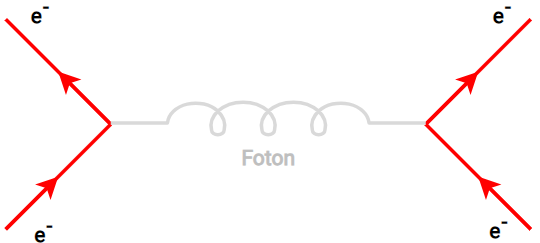
El diagrama anterior es algo parecido con el de la imagen 1. Lo principal a destacar es la partícula liberada, siendo está un fotón; partícula que como ya sabemos no tiene masa y como en este campo no se incluye la teoría de color cuántica, es decir, si hay color, por ende hay masa. Esto no aplica con los fotones.
| Características de campos | ||
| Fuerza fuerte | Electromagnetismo | |
| Partícula de interacción | Gluon | Fotón |
| Gap | Hay gap | No hay gap |
| Fuerza del campo | Partículas Confinadas | f ⁓ kq1q1/distancia2 |
| Rompimiento de equilibrio | Partículas Confinadas | Ionización |
| Carga | Eléctrica | Color |
| Auto interacción | Sí | No |
Otras características a destacar, la fuerza y partículas electromagnéticas conforman átomos y dichos átomos conforman moléculas, pudiendo generar así un proceso inverso, incluyendo más moléculas o metiendo energía, es decir ionizando al sistema; en su defecto la fuerza fuerte no puede ocurrir dicho proceso
Por último, en la interacción electromagnética el fotón no interactúa en el sistema; por otra parte, el gluon generado cambia la estructura del sistema.
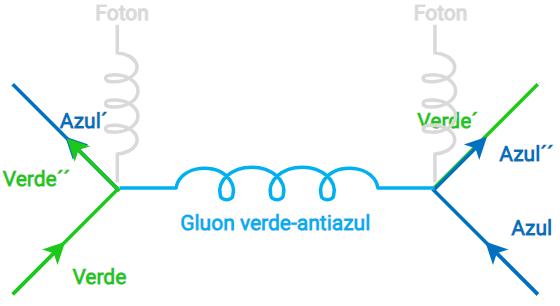
Interacciones de las 4 fuerzas universales.
Es fácil entender la fuerza de gravedad y el como está interactúa, siendo que está tiene un amplio alcance y una fuerza relativamente baja. En el caso de la electromagnética yace sentido, ya que conforme pasa el tiempo baja el magnetismo y aumenta la eléctrica, la cual genera más energía magnética; conforme pasa el tiempo baja la eléctrica y aumenta la magnética, la cual genera más energía eléctrica; entrando así en un bucle de alcance infinito – Está es la misma explicación por la que la luz viaja en el vació. A diferencia de las dos anteriormente mencionadas, las fuerza fuerte y débil no cumplen está característica de alcance.
En estudios de la Organización Europea para la Investigación Nuclear(CERN) se ha investigado que si se añade cantidades altas de energía a la fuerza débil, está puede llegar a tener altas relaciones con la fuerza electromagnética, es decir en vez de considerar dos fuerzas opuestas, se considera una sola llamada “Fuerza electrodébil”. Está investigación ha generado la teoría que en el principio del universo las 4 fuerza estaban unificadas.
| Interacción | Mediadores | Fuerza | Alcance |
| Fuerza | Gluones | 1038 | 10-15 |
| Electromagnética | Fotones | 1036 | ∞ |
| Débil | Bosones W y Z | 1025 | 10-18 |
| Gravedad | Gravitones (Hipoteticos) | 1 | ∞ |
Geometría diferencial de Yang-Mills.
Considerando la ecuación de la intensidad del campo de acción de Maxwell AF=dA.
$$-\int \frac{1}{2} F∧*F→-\int \frac{1}{4} F_{\mu v}F^{\mu v}d^4x$$
$$-\int \frac{1}{2} F∧*F +A∧*J →\int \left(-\frac{1}{4} F_{\mu v}F^{\mu v}+A_\mu J^\mu\right)d^4x$$
Lo anterior se pude convertir a la Lagrangiana, siendo remplazafas por las ecuaciones de Yang-Mills, d(*F)=J y dF=0.
$$L=\frac{1}{4g^2} \int Tr F ∧*F$$
Como anteriormente se menciono que cierta interacción del gluon viaja a la velocidad de la luz, también podemos considerarla como una partícula relativista, para así poder calcular su energía. Calculando dicha energía, podríamos obtener una aproximación más correcta del salto de masa generado en el instante.
$$E=\frac{p^2}{2m}+ V(x)+C \text{ – Energía clásica}$$
$$E^2=p^2c^2+m^2c^4 \text { – Energía relativista.}$$
Cuestiones del mass gap.
Sentadas algunas bases de la física moderna, se pueden realizar las siguientes preguntas.
¿Porqué la fuerza fuerte tiene un alcance corto?, ¿Será el massgap?
¿Porqué hay algunas partículas sin masa?
¿Cómo se verán los quarks puros?
¿Dónde surge el color compuesto?
Resolver el problema de Yang-Mills ayudaría en la interpretación matemática, puesto que los físicos ya entienden dichas incertidumbres de manera experimental.
Referencias
https://www.nationalgeographic.com.es/ciencia/7-problemas-matematicos-millon-dolares_18751
Yang-Mills & the Mass Gap – Clay Mathematics Institute. (2023, 24 mayo). Clay Mathematics Institute. https://www.claymath.org/millennium/yang-mills-the-maths-gap/
Yang-Mills existence and mass gap – Clay Mathematics Institute. (2022, 8 abril). Clay Mathematics Institute. https://www.claymath.org/lectures/yang-mills-existence-and-mass-gap/
Los 7 problemas del milenio
https://aeifmx.com/el-problema-de-p-versus-np/
https://aeifmx.com/la-hipotesis-de-riemann/
https://aeifmx.com/yang-mills-y-el-salto-de-masa-mass-gap/
https://aeifmx.com/ecuaciones-de-navier-stokes/
https://aeifmx.com/la-conjetua-de-birch-y-swinnerton-dyer/
https://aeifmx.com/la-conjetura-de-hodge/
https://aeifmx.com/conjetura-de-poincare/