La conjetura de Hodge
En el año 2000 la fundación Clay de matemáticas fundó los 7 problemas del milenio, los cuales tienen una recompensa de un millón de dólares para la persona que logre resolver un problema, en los que se encuentran: P vs NP, La conjetura de Birch y Swinnerton-Dyer, Yang-Mills y el salto de masa, Las ecuaciones de Navier-Stokes, La conjetura de Hodge, La hipótesis de Riemann y la Conjetura de Poincaré. En este artículo se profundizará la Hipótesis de Riemann.
La conjetura de Hodge se sitúa en la intersección de dos ramas de las matemáticas: la geometría diferencial y la geometría algebraica. Fue formulada por el matemático escocés William Hodge durante el Congreso Internacional de Matemáticos de 1950, celebrado en Cambridge. Se trata de una de las teorías más abstractas y desafiantes en el ámbito matemático.
En su esencia, la conjetura indaga sobre la posibilidad de aproximar la forma de un objeto determinado mediante la construcción progresiva de bloques simples de dimensiones crecientes. A día de hoy, esta conjetura sigue siendo un problema sin resolver. No hay consenso claro sobre si su solución se encontrará a través de técnicas de geometría algebraica o geometría diferencial. De hecho, dentro de la comunidad matemática, existe cierta división respecto a la viabilidad de demostrar o refutar esta teoría.
La conjetura de Hodge como problema del milenio
En términos generales, la conjetura busca comprender la estructura geométrica de variedades algebraicas, que son conjuntos de soluciones de ecuaciones polinómicas. Se centra en la relación entre las propiedades topológicas (relacionadas con la forma y la estructura del espacio) y las propiedades algebraicas (relacionadas con las ecuaciones polinómicas que describen la variedad).
Sea X una variedad compleja conexa de dimensión compleja n. Luego X, es una variedad diferenciable orientable de dimensión 2n, por lo que sus grupos de cohomología residen en grados cero a través de 2n. Asúmase que X es una variedad de Kähler, por lo que hay una descomposición en su cohomología con coeficientes complejos:
Recordamos que una estructura pseudocompleja en una variedad C∞ X de dimensión 2N es una estructura de módulo C en el haz tangente TX. Tal estructura de módulo induce una acción del grupo C* en TX, con λ ∈ C* actuando por multiplicación por λ. Por transporte de estructuras, el grupo C∗ actúa también sobre cada potencia exterior
∧nTX, así como en el dual complejado Ωn := Hom(∧nTX, C). Para p + q = n, aLa forma (p, q) es una sección de Ωn en la que λ ∈ C∗ actúa por multiplicación por λ−pλ¯−q
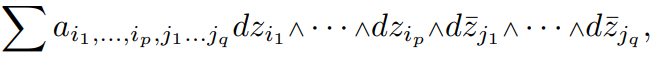
La descomposición Ωn = ⊕Ωp,q induce una descomposición d = d’ + d” de la diferencial exterior
Tomar productos exteriores de estos representantes armónicos se corresponde con el cup product en cohomología, por lo que cup product es compatible con la descomposición de Hodge:
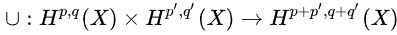
Dado que X es una variedad compleja, X tiene una clase fundamental.
si x es compacto y admite una métrica de Káhler, por ejemplo si X es un proyectivo variedad algebraica no singular, esta acción de C∗ en las formas induce una acción en cohomología, es decir, n formas para el modulo para el espacio cerrado Hn(x,C*) para formas exactas, siendo Hp,q para el espacio cerrado ed (p,q)-varedad
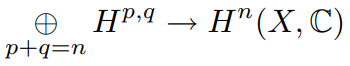
La clase cl(Z) en H2p(X, Z) es por tanto de tipo (p, p), en el sentido de que su imagen en
h2p(X, C) es. Las clases racionales (p, p) se denominan clases de Hodge. ellos forman el grupo
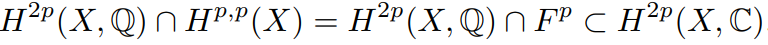
En una variedad algebraica proyectiva no singular sobre C*, cualquier
La clase de Hodge es una combinación lineal racional de clases cl(Z) de ciclos algebraicos.
Detección de las clase de Hodge
Sea (Xs)s∈S una familia algebraica de variedades algebraicas proyectivas no singulares: las fibras de un mapa proyectivo y suave f : X → S. Suponemos que está definido sobre la clausura algebraica Q¯ de Q en C. No se conoce ningún algoritmo para decidir si un determinado
Cohomologia de rham
Para la algebra conmutativa,
Ωp(U) con un diferencial, de tal manera que, d : Ωp(U) −→ Ωp+1(U), d ◦ d = 0 y siendo d derivación. Así, se dice que (Ωp (U), d) es un álgebra diferencial graduada, y se llamará el complejo de De Rham de U.}
Dada una variedad M, defnimos su k-ésimo espacio vectorial de cohomología de De Rham como el cociente
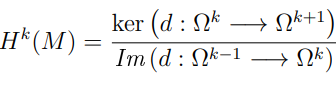
Aplicaciones
- Geometría Algebraica y Topología. Profundizar la comprensión de la relación entre la topología y la geometría algebraica, proporcionando herramientas más precisas para estudiar las propiedades geométricas de las variedades algebraicas.
- Física teórica. La geometría algebraica y la topología tienen aplicaciones en la física teórica, especialmente en teorías de cuerdas y geometría no conmutativa. Un avance en la Conjetura de Hodge podría tener implicaciones en estos contextos
Referencias
https://www.nationalgeographic.com.es/ciencia/7-problemas-matematicos-millon-dolares_18751
https://metode.es/wp-content/uploads/2017/06/93ES-MONO-4-conjetura-hodge.pdf
https://mate.dm.uba.ar/~pzadub/Clases/2016/1-geodif/notas.pdf
https://www.claymath.org/wp-content/uploads/2022/06/hodge.pdf
https://repositorio.escuelaing.edu.co/bitstream/handle/001/499/Castrell%C3%B3n%20Torres%2C%20Jairo%20-%202016.pdf?sequence=1&isAllowed=y
http://PEREZ_Cohomología
https://es.wikipedia.org/wiki/Cohomolog%C3%ADa
Redirect notice. (s. f.). https://www.google.com/url?sa=i&url=http%3A%2F%2Fb3ck.blogspot.com%2F2015%2F02%2Fcomplejos-de-de-rham-y-cohomologia.html&psig=AOvVaw0hxJEP4vIfBGa9RAljdW3T&ust=1702078370955000&source=images&cd=vfe&opi=89978449&ved=0CBEQjRxqFwoTCKirxJ6-_oIDFQAAAAAdAAAAABAD
Los 7 problemas del milenio
https://aeifmx.com/la-conjetua-de-birch-y-swinnerton-dyer/
https://aeifmx.com/ecuaciones-de-navier-stokes/
https://aeifmx.com/yang-mills-y-el-salto-de-masa-mass-gap/
https://aeifmx.com/la-hipotesis-de-riemann/
https://aeifmx.com/el-problema-de-p-versus-np/

