El problema de P vs NP.
La fundación Clay de matemáticas en el año 2000 fundó “Los 7 problemas del milenio”, los cuales tienen una recompensa de un millón de dólares para la persona que logre resolver un problema. En los que se encuentran: El problema de P vs NP, La conjetura de Birch y Swinnerton-Dyer, Yang-Mills y el salto de masa, Las ecuaciones de Navier-Stokes, La conjetura de Hodge, La hipótesis de Riemann y la Conjetura de Poincaré.
En este artículo se profundizará el problema de P igual a NP. Problema del milenio el cual tiene el propósito de la creación de algoritmos computacionales, cuya solución sea rápida al igual que su comprobación.
El problema de P vs NP como problema del milenio.
La interrogante inicial acerca de la relación entre las clases de complejidad NP y P fue planteada por el científico computacional Stephen Cook. Hasta la fecha, la teoría de la complejidad computacional no ha logrado proporcionar una respuesta definitiva. En esencia, la cuestión central, formulada como <<¿es P = NP completo?>>, indaga si la capacidad de “verificar” soluciones de manera rápida (característica de problemas NP) implica necesariamente la habilidad de “obtener” respuestas con la misma rapidez (atributo de problemas P). En este contexto, “rápidamente” significa “Tiempo polinómico”.
Encontrar una solución a este problema planteado hace 50 años podría desbloquear innumerables retos computacionales o demostrar que están fuera de nuestro alcance para siempre. Analizamos su histórica y su enorme impacto, que lo ha convertido en uno de los siete “Problemas del Milenio”.
Shiobhan Roberts.
La informática se encuentra ante la complejidad de diversos desafíos que marcan su evolución. Entre estos desafíos, destacan:
- Almacenamiento: Con el crecimiento exponencial de los datos, la gestión efectiva de grandes conjuntos de datos, su almacenamiento, procesamiento y análisis se ha convertido en un desafío clave.
- Tiempo: A través de una aproximación al número de pasos de ejecución que un algoritmo utiliza para resolver un problema.
Problemas del tipo P.
Conjunto de problemas que un ordenador puede resolver en un tiempo razonable. En particular, los problemas de la clase P son aquellos cuyo tiempo para encontrar una solución puede expresarse mediante una fórmula polinómica, como n2. En algoritmos de tiempo polinómico, donde n es el tamaño del problema o del input, el abordaje de este problema ocurre a una tasa de tiempo razonable.
Podemos expresar lo anterior como: P(x) = ax2 + bx + c, siendo así un tipo de problema que no supera un polinomio de grado 2.
Algunos ejemplos son:
- Ordenar una lista.
- Buscar un elemento de un texto.
- Multiplicación de número enteros.
Problemas del tipo NP.
Conjunto de problemas complejos y tardíos. En este caso nos referimos que son problemas de forma exponencial nx, donde x es cualquier valor mayor que 2; más sin embargo, la comprobación del problema se puede linealizar de forma x≤2. Es decir un problema del tipo x ∈ R | x ≥ 2, con comprobación x ∈ R | x ≤ 2.
Algunos ejemplos son:
Sudoku.
Rompecabeza.
Problema del viajero.
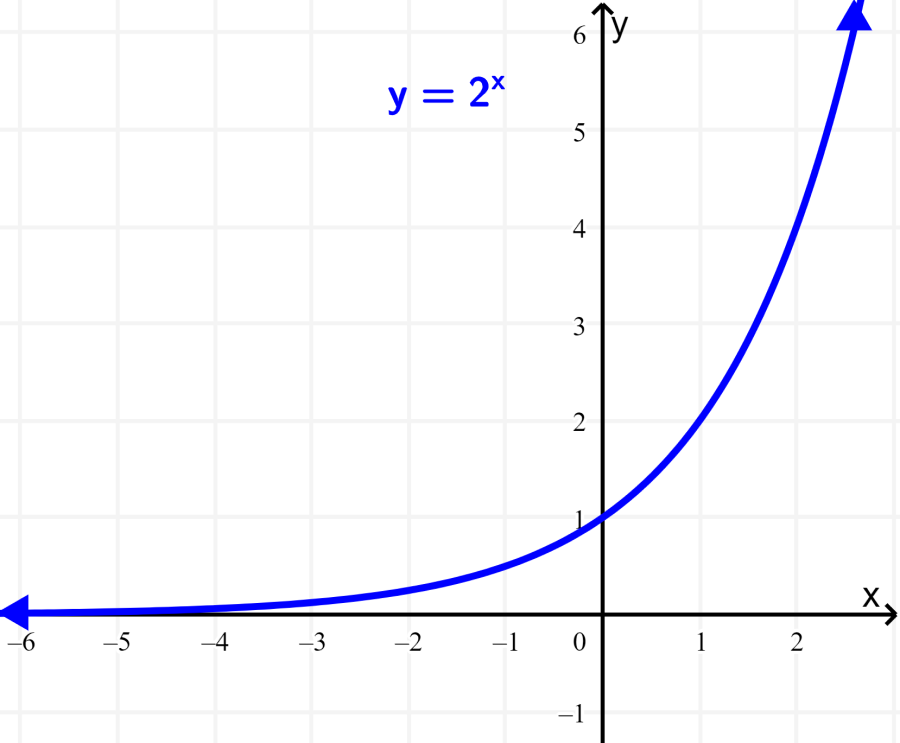
Visto desde la maquina de Turing.
Sea L un lenguaje definido sobre un alfabeto finito, Σ. Si existe una relación binaria R ⊂ Σ* × Σ* y un entero positivo k, tal que para todo x ∈ Σ*, se satisfacen las siguientes condiciones:
- x ∈ L ↔ ∃y ∈ Σ* tal que (x,y) ∈ R y |y| ∈ O(|x|k).
- LR={x#y : (x,y) ∈ R} en Σ ∪ {#}, donde es decidible por una maquina de Turing en tiempo polinomial.
Entonces, la máquina de Turing que decide LR es llamada el Verificador para L y y es llamado el Certificado de membresía de x en L. Finalmente, L se encuentra en NP “si y solo si” LR corre en tiempo polinómico.
¿P=NP?
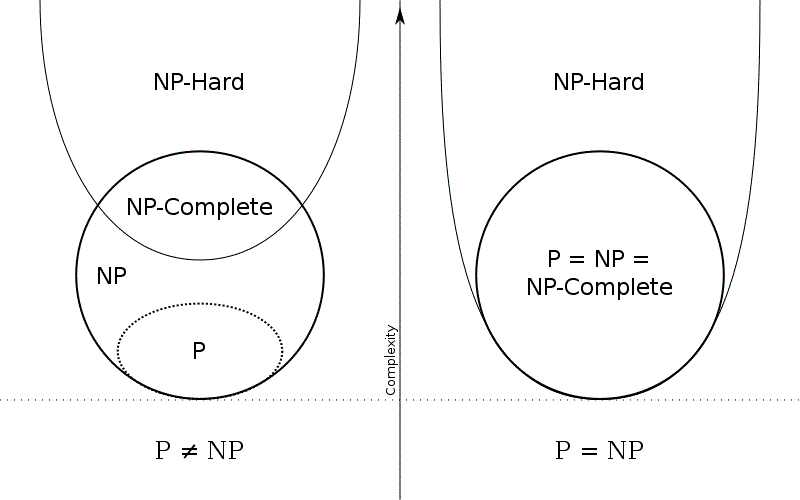
Entonces solo existen dos caminos P=NP o P≠NP.
Para P≠NP, se representa como: P∩NP. Donde si P≠Np, entonces queda demostrado que la mayoría de problemas se tendrían que resolver de forma tardía.
Para P=NP, se representa como: P⊂NP. Donde si P=NP, entonces se tiene un problema de resolución rápida y efectiva, y a su vez, una comprobación de la misma forma.
Comprobar dichas propiedades es lo que no han logrado demostrar los matemáticos ni los grandes programadores, pero ya se han tenido grandes avances de dicho estudio.
Teorema de Cook-Levin y el SAT.
El teorema de Cook-Levin propuesto en 1971. Establece que un problema de decisión, se puede reducir a un problema de satisfacción booleana (SAT). Esto quiere decir que problemas de decisión se pueden resolver mediante este sistema.
Considerando un problema NP-completo, podemos reducir la complejidad del mismo mediante el SAT. Dando mayor facilidad para la resolución del problema. A pesar de que reduce el problema, “no logra resolverlo por completo”.
Referencias
- The Clay Math Institute Millennium Prize Problems
- The Clay Math Institute Official Problem Description (pdf)
- Gerhard J. Woeginger. The P-versus-P page. A list of links to a number of purported solutions to the problem. Some of these links state that P equals NP, some of them state the opposite. It’s probable that all these alleged solutions are incorrect.
- Computational Complexity of Games and Puzzles
- Scott Aaronson’s Complexity Zoo: P
- Qeden, wiki that aims to solve the Millennium Prize Problems
- Scott Aaronson’s Shtetl Optimized blog: Reasons to believe, a list of justifications for the belief that P ≠ NP
- https://www.nationalgeographic.com.es/ciencia/7-problemas-matematicos-millon-dolares_18751
- P «vs» NP, el dilema matemático que creó la complejidad computacional. (2021, 3 diciembre). MIT Technology Review.
- Villatoro, F. R. (2017, 13 noviembre). Mi opinión sobre la demostración P≠NP de Norbert Blum – La ciencia de la mula Francis. La Ciencia de la Mula Francis. https://francis.naukas.com/2017/08/15/mi-opinion-sobre-la-demostracion-p/
- D, S. (2023, 8 octubre). Teorema de Cook-Levin (sobre la NP-completitud de SAT). Club de los Teoremas. https://www.teoremas.club/teorema-de-cook-levin-sobre-la-np-completitud-de-sat-2/#:~:text=El%20Teorema%20de%20Cook%2DLevin%20fue%20propuesto%20por%20Stephen%20Cook,un%20algoritmo%20de%20satisfacci%C3%B3n%20booleana.
Los 7 problemas del milenio.
https://aeifmx.com/el-problema-de-p-versus-np/
https://aeifmx.com/la-hipotesis-de-riemann/
https://aeifmx.com/yang-mills-y-el-salto-de-masa-mass-gap/
https://aeifmx.com/ecuaciones-de-navier-stokes/
https://aeifmx.com/la-conjetua-de-birch-y-swinnerton-dyer/
https://aeifmx.com/la-conjetura-de-hodge/
https://aeifmx.com/conjetura-de-poincare/

