Qubits de luz y materia: la importancia de los polaritones en el desarrollo de la física computacional
Artículo con mención honorífica en el II Concurso de Artículos Divulgativos: Explora y Escribe (agosto - septiembre, 2024). AUTOR: José Fernando López Fuentes
Los polaritones surgieron de forma teórica a mediados del siglo XX, pero no fue hasta principios de 1980 donde se permitieron las condiciones de creación en laboratorios de estas cuasipartículas. Hoy en día, el estudio de los polaritones ha generado múltiples disciplinas que buscan aplicar sus principales características de interacción luz-materia teniendo como consecuencia constantes innovaciones en la física de materiales y mecánica cuántica.
Polaritones, exitones y microcavidad óptica
Una microcavidad óptica tiene la función de retener la luz en orden de su longitud, es decir, retiene la luz en volúmenes sumamente pequeños entre dos reflectores permitiendo que los fotones encerrados interactúen con la materia, pozos cuánticos y nanoestructuras, lo que da paso un fenómeno de acoplamiento. Sin embargo, en la realidad no es posible encerrar toda la luz. De esta manera surge el concepto de factor de calidad que representa la relación entre la frecuencia del fotón almacenado y la tasa de su escape; esto divide el panorama en dos partes: acoplamiento fuerte y débil (García, 2022). La luz confinada en los microresonadores (dos espejos) cede energía a un material bidimensional (grosor del orden de micras) Y esta energía es la suficiente para liberar un electrón del material y generar una vacancia (hueco) de carga positiva. A esta interacción entre el hueco y el electrón libre se le conoce como exitón. En otras palabras, un exitón es el estado excitado de un simiconductor en el que el electrón que se encuentra en la banda de conducción está ligado a un hueco; debido a que el electrón y el hueco tienen cargas opuestas, el electrón es atraído y terminar por ocupar el hueco nuevamente, por consiguiente, la luz confinada vuelve transferir energía para soltar nuevamente un electrón. Este ciclo ocurre periódicamente, lo que da el nacimiento de los polaritones, éstas son cuasipartículas (luz-materia) que no existe por sí sola, sino que su origen radica en todo un sistema acorde del acoplamiento fuerte de la interacción hueco-electrón dándole algunas propiedades de luz y materia (Gonzales, 2020).
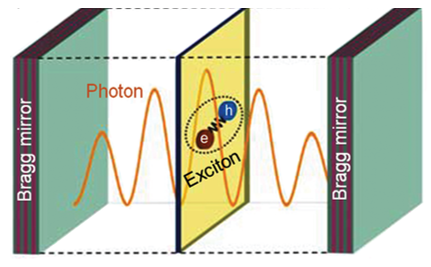
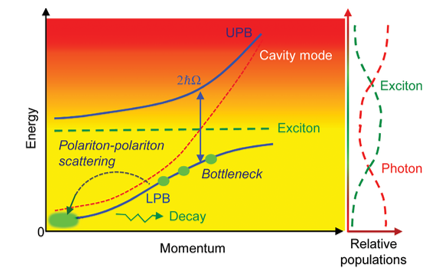
Fig. 1. a) Los polaritones surgen de un fuerte acoplamiento entre el excitón y el modo fotónico de una microcavidad. b) Dispersión, proceso dinámico y fracciones de fotones y excitones de las ramas de polaritón (García, 2022).
Esta partícula le permite comportarse como una colección de fotones confinados con masa; evidentemente, los fotones no poseen masa, por lo que se les adquiere una relación de dispersión que indica la masa efectiva, dándole un carácter bosónico, lo que le permite generar condensado y superfluidos. De igual manera, al enfriarlo le permite alcanzar la transición del condensado de Bose-Einstein (Torres, 2019).
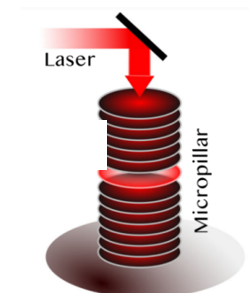
Para poder manipular los polaritones, se usan los micropilares, que son estructuras nanofotónicas a partir de semiconductores que tienen la función de confinar las microcavidades una tras otra, lo que les permite interactuar entre polaritones, lo que da paso a los modos de energía, que hacen referencia a los estados cuánticos de energía en que se encuentran los polaritones, siendo el modo de menor energía la que le permite formar los condensados de Bose-Einstein (García, 2022).
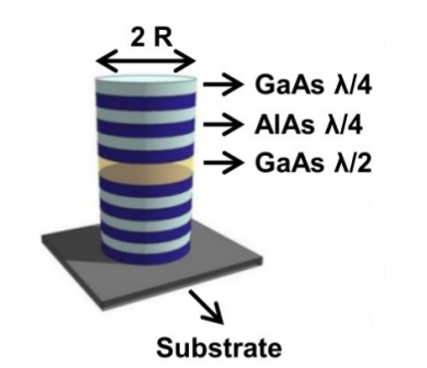
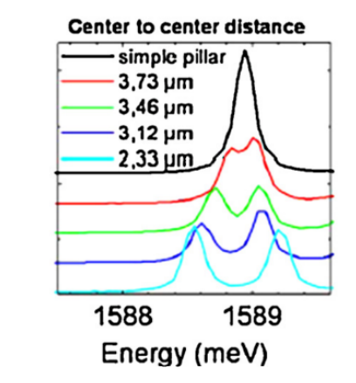
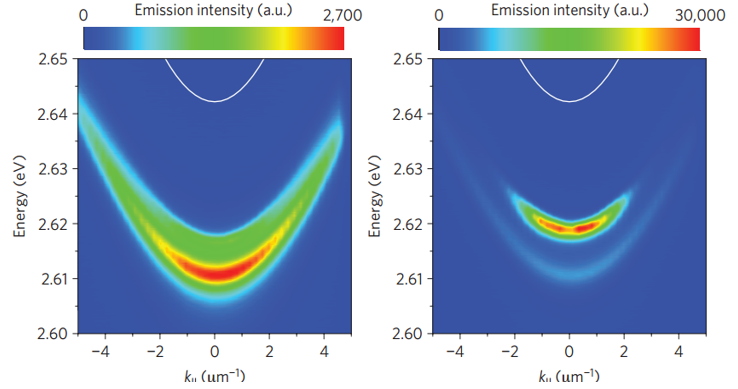
Fig. 2. a) Esquema de la configuración para un micropilar con radio de 1.5µm, formado por 10 capas λ/4 de GaAs en sus espejos de Bragg b) Podemos apreciar el espectro del menor estado de energía (línea negra) para un solo micropilar, y de dos micropilares acoplados con distintas distancias de centro a centro (Amos, 2016).
Computación cuántica
Las computadoras convencionales trabajan principalmente bajo el concepto de bit, siendo éste la unidad mínima de información, la cual tiene únicamente dos posibles valores como compuerta lógica (0 o 1). Sin embargo, en la computación cuántica, se transciende el concepto del bit al qubit, la cual se comporta como estados cuánticos entre los mismos valores de 0 y 1 al ser observado, sin embargo, también permite valores disantos a éstos o en superposición en una combinación lineal (Ruiz, 2020):
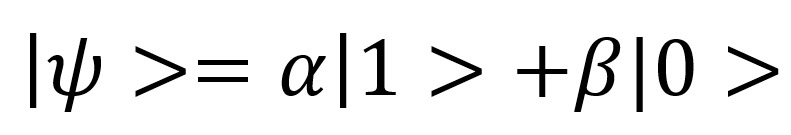
dónde |1> y |0> son los vectores base y forman una base ortogonal. Ambos cumplen su condición de normalización para α y β, lo que al observar el qubit tiene una probabilidad a^2 para 1 y b^2 para 0.
La información de un qubit es transmitida y las compuertas lógicas cuánticas ejecutan manipulaciones sobre esta información. Estas compuertas son matrices de diferentes tamaños en la que cada una hace alguna operación sobre la información. Algunos ejemplos de compuertas son la matriz identidad, las compuertas de Pauli, compuerta NOT cuántica, etc.. Estas operaciones tienen que realizarse antes que se disipen los polaritones, con el uso de un pulso láser de frecuencia temporal menor al de la vida de un polaritón para evitar pérdidas de información. Debido a su naturaleza fotónica, los polaritones pueden ser manipulados a velocidades extremadamente altas, facilitando operaciones cuánticas rápidas. La combinación de propiedades de luz y materia permite el uso de técnicas ópticas avanzadas para manipular estados cuánticos.
Los condensados de polaritones dentro de micropilares tienen diversas ventajas con respecto a otros sistemas donde se realizan qubits. Claramente, la temperatura a la cual se pueden realizar la creación de qubits por medio de micropilares es más conveniente en comparación con las islas superconductoras, aparte de la sencilla manipulación de los micropilares por medio de los bombeos láser.
Evidentemente, el mayor de los retos es lograr estos condensados de Bose-Einstein de polaritones a temperatura ambiente mientras conserve todas sus propiedades, por ello, se han realizado varios proyectos orientados a esta problemática. Por ejemplo, el grupo de investigadores del Centro de Nanotecnología Binnig y Roherer de IBM fabricaron por primera vez un condensado a valor ligeramente mayores de 300K por un tiempo de vida muy corto (aproximadamente 200 femtosegundos), Esto se logró al generar microcavidades con un polímero (MelPPP) entre los dos espejos, en donde se aplica una pulso de luz cada 8 picosegundos; esto causa la liberación de electrón del polímero para generar el polaritón con una masa efectiva lo suficientemente pequeña (una billonésima parte de un átomo) para formar el condensado.
.
.
r e f e r e n c i a s – y – f u e n t e s – c o n s u l t a d a s
- Ghosh, S. (2020). Quantum computing with exciton-polariton condensates. npj Quantum Information.
- Amos, A (2016). Exciton-polaritons in lattices: A non-linear photonic simulator. Comptes Rendus Physique.
- García, P. (2022). Compuertas lógicas cuánticas en fluidos polaritónicos. Recuperado de: https://miguelbastarrachea.com/wp-content/uploads/2022/07/Pedro_Garcia_PT1_22I.pdf
- Torres, A. (2019). Fabricación y caracterización de microcavidades ópticas de silicio poroso. Recuperado de: http://www.fc.uaslp.mx/pca/tesis/2019Maestria/TorresRosalesAngelAndresTesis-Maestria201994.pdf
- Villatoro, F. (2013). IBM fabrica un condensado de Bose-Einstein a temperatura ambiente. Recuperado de: https://francis.naukas.com/2013/12/11/ibm-fabrica-un-condensado-de-bose-einstein-temperatura-ambiente/
- Gonzales, P. (2020). Condensado de polaritones. Recuperado de: https://digital.csic.es/bitstream/10261/247637/1/condesatones.pdf
- Ruiz, R. (2020). Dinámica de un cubit poliatómico con bajo consumo de energía.
- Imagen de la portada realizada con leonardo.ai

