¿Por qué los múltiplos de 5 terminan en cinco o cero? – Una introducción a la aritmética modular

Publicado el

Es probable que muchos de nosotros cuando aprendimos las tablas de multiplicar de pequeños, nos llegamos a preguntar: ¿qué patrones existen en los múltiplos de cada tabla de multiplicar?
Claramente no lo planteábamos de esa manera, si no que nos deteníamos a revisar si cada tabla de multiplicar contenía a todos los números del cero al nueve en la parte de las unidades. Es bien sabido que los múltiplos de 3 poseen a cada dígito del cero al nueve en sus terminaciones. Sin embargo, el número 5 es más limitado, pues sólo puede terminar en dos dígitos diferentes (cero o cinco). Si uno fue un poco más curioso, se habrá preguntado por qué sucede esto, y por qué algunos números tienen más libertad mientras que otros están más restringidos. La respuesta la podemos encontrar en un campo de las matemáticas que a menudo es olvidado: la teoría de números. Más específicamente, a una rama esencial de esta área, la aritmética modular.  

La teoría de números inició en la antigua Grecia. Los griegos tenían un particular interés (y un espectro limitado) por los números enteros, y las propiedades aritméticas que poseen. No obstante, la teoría de números se consolidó con Diofanto, cuando planteó un tipo de ecuaciones ahora conocidas como las ecuaciones de Diofanto. Estas ecuaciones son similares a las ecuaciones a las que estamos acostumbrados, con la característica de que, en la teoría de números, se busca hallar únicamente las soluciones enteras a dichas ecuaciones. Tomemos de ejemplo a la ecuación 7x + 5y = 1. De esta podemos obtener una solución entera para la ecuación x = -2 y y = 3. Si bien no es la única solución, Diofanto no estaba interesado en todas las soluciones reales a las ecuaciones, únicamente a las soluciones enteras. 

Imagen 1. Algunas soluciones a la ecuación de Diofanto 7x + 5y = 1

Esto nos introduce al pilar fundamental de la teoría de números: los números primos. Los números primos son los cimientos de la teoría de números, y particularmente de la aritmética modular. Estos facilitan el trabajo con números enteros, y hacen uso del residuo como un auxiliar para evitar caer fuera de estos. 

Números primos

Antes de entrar en materia, definiremos qué son los números primos. De acuerdo con Pommersheim, Marks y Flapan (2010), un número primo es aquel que no tiene otros factores positivos además de sí mismo y el 1. Esto quiere decir que, si se intenta dividir a un número primo por un número diferente a sí mismo o 1, el resultado no será entero. Como ya vimos, en la aritmética modular es muy importante que los resultados obtenidos sean números enteros, es por eso por lo que se también se trabaja con el residuo de la división de dos números enteros. Al trabajar de esta manera, los resultados están delimitados únicamente a números enteros. Como consecuencia de esto, llegamos a que podemos expresar a cualquier número de la siguiente manera: 

a = bc + r

Donde a es el dividendo, b es el divisor, c es el cociente y r es el residuo. 

Los números primos son sumamente importantes en la forma en la que hacemos matemáticas. Todos los números pueden ser descompuestos como un producto de únicamente números primos, y, además, dicha combinación de números primos es exclusiva para cada número. 

Por ejemplo, el número 39 puede ser reescrito como el producto de 3×13. Tanto el 3 como el 13 son números primos, y esta combinación de números primos es exclusiva para el número 39. Esta propiedad de los números tiene un nombre, y se le conoce como el teorema fundamental de la aritmética. 

Congruencia

Otro concepto clave de la teoría de números es la congruencia. Formalmente se dice que: “dados tres números: a, b y n, decimos que a es congruente a b modulo n si n divide a la resta de a y b” (Pommersheim et al., 2010). En notación matemática esto se puede representar de la forma a≡b(mod n). En palabras más sencillas, se refiere a que, si tenemos dos números a y b, al ser divididos por un número n, al cual le llamamos el módulo, el resultado de dichas divisiones tendrá el mismo residuo. 

Por ejemplo, podemos comprobar si los números 34 y 54 son congruentes bajo el módulo 10. Podemos utilizar la definición de congruencia y notar que la diferencia de 34 y 54 (20 o –20, el orden no es importante), es un múltiplo de 10, por lo que se puede concluir que 34 y 54 son congruentes módulo 10. Sin embargo, otra manera de comprobarlo es dividiendo a ambos números entre 10; podremos notar que ambos comparten un residuo de 4, así que también podemos concluir que ambos números son congruentes módulo 10. Adicionalmente, las definiciones anteriores son mutuamente incluyentes, es decir, que un número n divida a la diferencia de dos números a y b implica que dichos números dejan el mismo residuo al ser divididos entre n, y viceversa. 

Aritmética modular

Esta forma de hacer operaciones se llama aritmética modular. Un ejemplo cotidiano y muy conocido es el código binario. Este sólo cuenta con 2 dígitos, el 0 y el 1, y cada vez que se cuenta hasta un múltiplo de 2, el contador se reinicia y regresa al cero. Podemos ver al código binario es como una suma de las potencias de 2 multiplicadas por el número escrito en el código. 

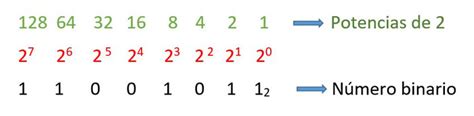
Imagen 2. Número binario representado como potencias de 2.

En el caso del código binario, podemos decir que su módulo es el número 2, sin embargo, se pueden crear conjuntos de números a partir de cualquier módulo. A estos conjuntos se les llama Zn, y usualmente son representados en manera de tabla para visualizar de mejor manera su lógica. 

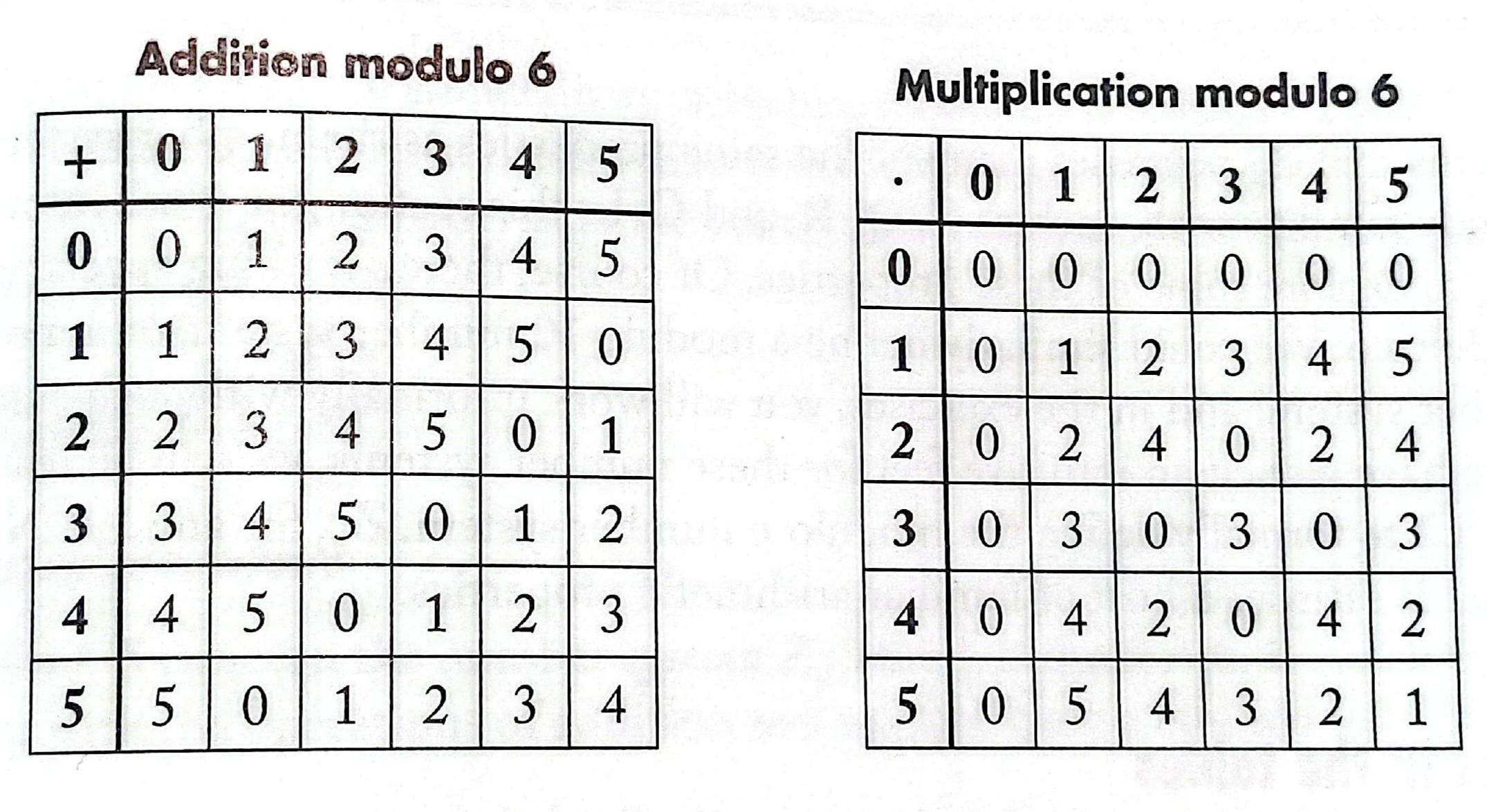
Imagen 3. Tablas de suma y multiplicación de Z6 

Si observamos, por ejemplo, en la tabla de la multiplicación, al multiplicar 2×3 que en nuestro sistema numérico es simplemente 6, en Z6 el resultado arroja un cero. Esto se debe a que 6 es el módulo de Z6, por lo que 5 es el número más grande que se puede obtener antes de volver al 0. En este sentido, el 0 en Z6 puede significar cualquier múltiplo de 6, ya que se cumple que el residuo de cualquier múltiplo de 6 es cero. 

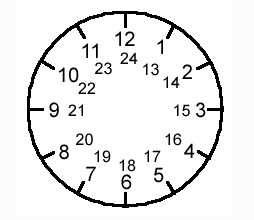
Otro caso de un sistema numérico modular es el reloj. Este maneja al módulo 12; es por eso por lo que, para nosotros, las 12 de la madrugada son también las 0 horas. Si uno es aún más observador, se podrá dar cuenta que la diferencia de cada pareja de números que comparte hora es igual a 12, lo cual significa que dichas parejas son, además, congruentes en módulo 12. Esto podrá parecer obvio, puesto que el reloj opera bajo el mismo módulo y cada hora está separada de su pareja equivalente por 12 horas, pero es sumamente útil a la hora de pensar en cómo se traducen las congruencias y la aritmética modular a nuestro sistema numérico. 

Imagen 4. Reloj módulo 12. Imagen original de Vicky Neale. 

Aritmética modular en criptografía 

Una de las aplicaciones más importantes de la teoría de números, y sobre todo de la aritmética modular ocurre en la criptografía. Las funciones hash y el cifrado RSA son formas de encriptar información de manera casi impenetrable. Estas funciones tienen la característica de que el receptor de la información no necesita conocer el código de antemano para decodificar el mensaje. El funcionamiento específico de estas funciones es el siguiente:  

Primero, cada uno debe configurar sus propios pares de claves y compartir la clave pública entre sí. Las dos entidades deben mantener en secreto sus claves privadas para que sus comunicaciones permanezcan seguras. 

Una vez que el remitente tiene la clave pública de su destinatario, puede usarla para cifrar los datos que desea mantener seguros. Una vez que se ha cifrado con una clave pública, solo se puede descifrar con la clave privada del mismo par de claves. Incluso la misma clave pública no se puede usar para descifrar los datos. […]. 

[…] Cuando el destinatario recibe el mensaje cifrado, utiliza su clave privada para acceder a los datos. Si el destinatario desea devolver las comunicaciones de forma segura, puede cifrar su mensaje con la clave pública de la parte con la que se está comunicando. Nuevamente, una vez que se ha cifrado con la clave pública, la única forma de acceder a la información es a través de la clave privada correspondiente. (Ciberseguridad, 2022).

Estas claves son generadas a partir de números primos. De manera muy resumida y simplificada, la función procura elegir un par de números primos muy grandes y separados entre sí, esto para evitar alguna relación evidente entre ambos números, y posteriormente elige un módulo para generar el código. Las especificaciones técnicas de este método están fuera del espectro de este artículo, sin embargo, nótese como dos de las técnicas más seguras del mundo para encriptar información, tienen sus bases en los conceptos básicos de la aritmética modular. 

Conclusiones

A pesar de ser una rama un tanto olvidada por las matemáticas y la ciencia en general, la teoría de números sigue siendo una parte importante de los avances tecnológicos actuales. Como ya vimos, la criptografía depende enormemente de la aritmética modular, y en general, la generación de claves y códigos únicos utilizan métodos similares al RSA y las funciones hash.  

La aritmética modular a su vez, incentiva un pensamiento diferente de las matemáticas, en especial de las operaciones a las que estamos acostumbrados a trabajar en nuestro sistema numérico como la suma y la multiplicación. Expandir nuestra visión hacia modelos matemáticos diferentes nos puede ayudar a encontrar soluciones a problemas de la vida cotidiana, e incluso a problemas trascendentes de la ciencia y la tecnología. 

Así que, por último, para responder a la pregunta del por qué los múltiplos de cinco únicamente terminan en cinco o cero, debemos recurrir a la aritmética modular, y darnos cuenta de que, en cierta manera, nuestro sistema numérico también es modular (aunque no del todo). Entonces, una manera modular de responder esta pregunta sería: porque los residuos de los múltiplos de 5 módulo 10 (debido a nuestro sistema decimal) siempre son cinco y/o cero. 

————– Bibliografía y fuentes consultadas ————–