Cómo los nudos nos ayudan a entender interrogantes de la ciencia moderna

Publicado el 
Artículo ganador del 2do lugar en el II Concurso de Artículos Divulgativos: Explora y Escribe (agosto - septiembre, 2024). AUTOR: Carlos Ortega Figueroa

En 1867, William Thomson (Lord Kelvin) propuso la teoría de que los átomos estaban compuestos por vórtices de éter que formaban nudos. Kelvin mencionaba que diferentes configuraciones de nudos correspondían a cada átomo de cada elemento. Mientras la teoría de Kelvin tomaba popularidad, Peter Guthrie Tait, quien trabajaba con Kelvin en ese tiempo, se dio a la tarea de investigar y enlistar los diferentes tipos de nudos que existen. Tait logró enlistar todos los nudos hasta aquellos que tienen 7 cruces y, después de que la teoría de Kelvin fuera eventualmente rechazada, los descubrimientos de Tait sirvieron como las bases para lo que ahora se conoce como teoría de nudos.

En las matemáticas, un nudo se forma cuando tenemos una cuerda que forma un ciclo cerrado y que no se interseca a sí misma. Si tomáramos un pedazo de cuerda, la amarráramos y después selláramos la cuerda, obtendríamos un nudo. A no ser que cortemos la cuerda sellada, el nudo debe ser imposible de desamarrar

Bajo esta lógica, el nudo más simple sería aquel que no tiene ningún cruce y es simplemente una cuerda circular. Este se conoce como “nudo trivial”. A este le sigue el nudo de tres cruces, también llamado “nudo trébol”.

El nudo trivial y el nudo de trébol son los 2 nudos más sencillos que existen
El nudo trivial y el nudo de trébol son los 2 nudos más sencillos que existen

Nudos primos y compuestos

En la teoría de nudos, un nudo primo es un nudo que no se puede descomponer en un nudo más simple. El nudo trébol es un ejemplo de un nudo primo de 3 cruces. Si unimos 2 nudos primos de tal manera que ambos formen un ciclo cerrado, pero sin alterar la estructura del nudo (podemos imaginar que cortamos ambas cuerdas y las sellamos con dos nudos combinados), obtenemos un nudo compuesto. Como todos los nudos compuestos están hechos de nudos primos, los investigadores se dedican principalmente a tabular a los nudos primos.

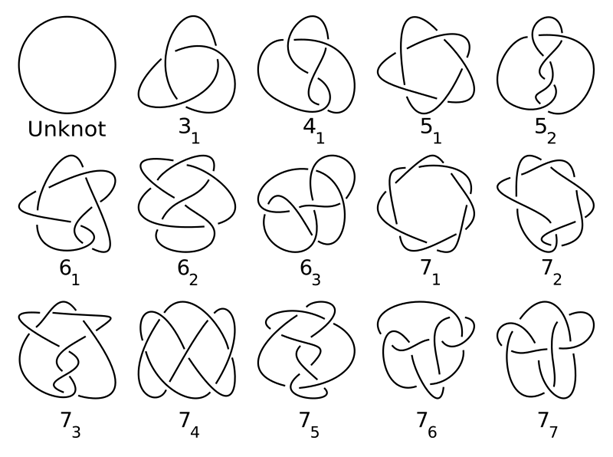
Tabla de los nudos primos de hasta 7 cruces
Tabla de los nudos primos de hasta 7 cruces

Los cruces son muy importantes cuando se estudia la teoría de nudos. Es lo que diferencia a cada nudo de los demás. Un cruce es aquella parte del nudo en que la cuerda pasa por encima o por debajo de sí misma. Sin embargo, el número de cruces de un nudo no significa que ese nudo sea un nudo primo, pues se puede tratar de una proyección de otro nudo más sencillo. Tomemos el ejemplo del nudo trébol:

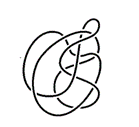
Una proyección del nudo trébol de 14 cruces
Una proyección del nudo trébol de 14 cruces

Aunque no lo parezca, el nudo anterior es un nudo trébol que fue deformado hasta 14 cruces para verse de esa manera. Pero si no es posible detectar a simple vista que un nudo sea diferente de otro, ¿cómo podemos estar seguros de que cualquier nudo no es simplemente una proyección del nudo trivial?

Movimientos de Reidemeister y tricolorabilidad

Para ayudarnos a diferenciar si diferentes proyecciones de un nudo pertenecen al mismo, utilizamos los movimientos de Reidemeister, propuestos por Kurt Reidemeister en 1927. Estos nos dicen que únicamente son necesarios 3 tipos de movimientos para transformar cualquier proyección de un nudo en otra. El primero de estos movimientos es hacer o deshacer un giro en la cuerda que conforma al nudo (Tipo I); el segundo movimiento es pasar un ciclo de cuerda por encima de otro (Tipo II), y el tercero consiste en pasar un pedazo de cuerda por encima o por debajo de un cruce (Tipo III).

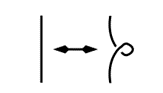
Movimiento de Reidemeister Tipo I
Movimiento de Reidemeister Tipo I
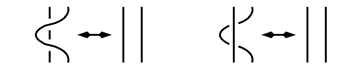
Movimiento de Reidemeister Tipo II
Movimiento de Reidemeister Tipo II

Si bien esto nos ayuda a saber cuándo 2 nudos son una proyección del mismo nudo, esto no nos asegura que 2 nudos a los que no hemos llegado por medio de movimientos de Reidemeister sean diferentes. Es posible que ambas proyecciones se traten del mismo nudo y que simplemente no hemos hecho los movimientos indicados para probarlo. A pesar de esto, los nudos sí poseen características individuales que los hacen diferentes de los demás nudos. Estas características son llamadas “invariantes”, y si bien existen invariantes que diferentes nudos comparten entre sí, si 2 nudos tienen una invariante diferente, entonces podemos afirmar con seguridad que esos 2 nudos son diferentes.

El número de cruces es una invariante, así como lo es la tricolorabilidad. La tricolorabilidad nos dice que un nudo (o una proyección de este) es tricolorable (o 3-coloreable) si podemos asignarle un color diferente a cada tramo de cuerda y que, en todos los cruces, dichos tramos sean todos del mismo color o todos de un color diferente. Se deben utilizar al menos dos colores cuando se pone a prueba la tricolorabilidad, de lo contrario podríamos colorear todo el nudo del mismo color y esto haría inválido el análisis para diferenciarlos. De esto podemos obtener solo dos resultados: ya sea que un nudo es 3-coloreable, o no lo es.

Hasta el momento no hemos demostrado que el nudo trivial y el nudo trébol son 2 nudos diferentes, pero, gracias a la tricolorabilidad, esto se convierte en un ejercicio sencillo. En el caso del nudo trivial, este no es 3-coloreable, ya que, al ser un solo segmento de cuerda, no podemos asignarle más de 2 colores. Por el contrario, el nudo trébol es fácilmente 3-coloreable, incluso si sus proyecciones tienen más de 3 cruces.

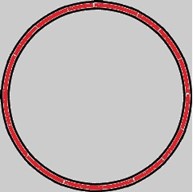
El nudo trivial no es 3-coloreable
El nudo trivial no es 3-coloreable
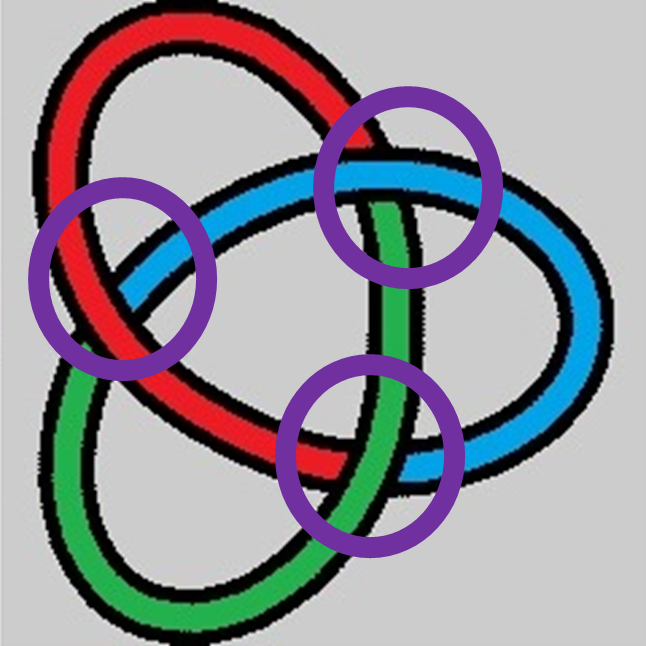
El nudo trébol claramente es 3-coloreable
El nudo trébol claramente es 3-coloreable
Proyección del nudo trébol. Obsérvese que, a pesar de tener más cruces, el nudo sigue siendo 3-coloreable
Proyección del nudo trébol. Obsérvese que, a pesar de tener más cruces, el nudo sigue siendo 3-coloreable

Como se puede observar, incluso las proyecciones de otros nudos que son 3-coloreables siguen el principio de tricolorabilidad. Como el nudo trivial no es 3-coloreable, mientras que el nudo trébol claramente lo es, podemos estar seguros de que el nudo trivial y el nudo de trébol son nudos diferentes.

Enlaces

Aunque hemos hablado de nudos que se hacen con un solo ciclo de cuerda, en la teoría de nudos también se consideran aquellos nudos que están compuestos por 2 o más ciclos, los cuales son llamados enlaces. El enlace más sencillo que existe es el enlace trivial, el cual no es más que 2 nudos triviales que no interactúan entre sí.

Enlace trivial
Enlace trivial

Uno de los enlaces más famosos son los anillos de Borromeo. Estos aparecen en varias referencias históricas y se trata de 3 nudos triviales enlazados.

Los anillos de Borromeo aparecen en el escudo de la Casa de Borromeo
Los anillos de Borromeo aparecen en el escudo de la Casa de Borromeo

Aplicaciones de la teoría de nudos en la ciencia

El ADN de las bacterias está formado por una molécula cíclica que se enreda en un nudo; las bacterias no pueden duplicarse si este ADN está enredado, por lo que utilizan una enzima que les permite cortar a la molécula para después volver a unirla y así conseguir duplicarse. Si este proceso falla, las bacterias no pueden replicarse y por consecuencia mueren. Este proceso se puede extrapolar a la teoría de nudos, y es el método que utilizan los antibióticos conocidos como quinolonas. Esta es solo una de muchas maneras en las que la teoría de nudos se aplica en la ciencia moderna.

Por ejemplo, cuando las moléculas se enredan en nudos adquieren propiedades nuevas. Estudios realizados por el químico de la Universidad de Manchester, David Leigh, lograron sintetizar una molécula enredada con 5 cruces que funciona como un catalizador; la molécula sintetizada en su estado original no posee propiedades catalizadoras.

“Ser capaces de crear nudos más complicados ayudará a los investigadores a probar como los nudos afectan la dureza, flexibilidad y otras propiedades de los materiales, y ayudará a determinar cuáles son los más adecuados dependiendo de la situación. Algunos expertos prevén un futuro en el que los nudos se combinarán para formar materiales con gran resistencia al calor o con propiedades catalizadoras. Otros esperan que algún día los nudos microscópicos sean usados como redes para una distribución segura de medicamentos en el cuerpo u otros micro cargamentos.” Cepelwicz (2018).

Incluso algo tan sencillo como el amarrarse las agujetas sienta sus bases en la teoría de nudos. Si amarramos nuestras agujetas en sentido antihorario, lo que estamos haciendo es amarrar 2 nudos trébol idénticos uno arriba del otro, formando un enlace que se conoce como el nudo de la abuela. Si por el contrario amarramos nuestras agujetas en sentido horario, lo que obtendremos es una imagen espejo de los 2 nudos trébol. A este enlace le llamamos nudo del cuadrado, el cual no se desamarra tan fácilmente como el nudo de la abuela.

Nudo de la abuela
Nudo de la abuela
Nudo del cuadrado
Nudo del cuadrado

Aunque aún queda mucho por descubrir en el campo de la teoría de nudos, es innegable que el avance obtenido hasta el momento nos ayuda a comprender mejor muchas áreas de la ciencia que de otra manera no tendríamos forma de investigar. Solamente se han logrado sintetizar un par de nudos de los 352 152 252 que se han descubierto, y si bien la gran mayoría de estos nudos son muy difíciles de sintetizar con la tecnología actual, es posible que en algunos años la teoría de nudos esté más presente en nuestras vidas de lo que imaginamos. El futuro de la teoría de nudos es prometedor, y es emocionante el imaginar que, en algunos años, todos estos conceptos que nos parecen tan abstractos serán la única respuesta a muchas de las incógnitas de las áreas más importantes de la ciencia.

.

.

r e f e r e n c i a s – y – f u e n t e s – c o n s u l t a d a s